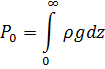 |
A pressão é o peso da coluna de ar acima do ponto considerado. Aplicando derivada parcial com respeito ao tempo, usando a equação da continuidade e integrando o termo da componente vertical, chega-se a:
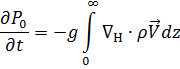 |
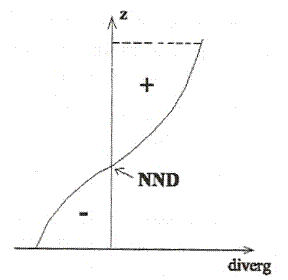
Isto significa que a tendência da pressão em superfície pode ser estimada a partir da divergência integrada na coluna. Mas, para que haja abaixamento da pressão na superfície deve haver uma diminuição de massa na coluna de ar, o que só é fisicamente viável se o perfil vertical de divergência apresentar maior divergência do que convergência.
 |
O problema é que as estimativas de divergência possuem muitos erros devido a erros nas medidas de vento. Por exemplo, um erro de 10 % no vento pode levar a 100% de erro na divergência.
Na prática, a vorticidade é mais adequada para analisar este tipo de problema. Por simplicidade, veja a vorticidade geostrófica no plano f.
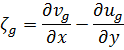 |
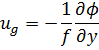 |
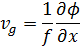 |
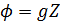 |
Sendo z a altura geopotencial.
Considerando f = f0:
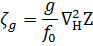 |
Cuja tendência é:
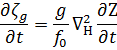 |
Na formação de baixa no HS:
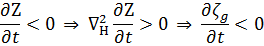 |
Sutcliffe aplicou sua teoria no nível de não divergência (NND), com a idéia de usar a estrutura térmica para este problema, através da equação do vento térmico. Esta aplicação se baseia nas seguintes suposições (adequadas para latitudes médias):
1) Existe NND em ~ 500 hPa (geralmente entre 400 e 600);
2) Vorticidade geostrófica ~ vorticidade real;
3) Vento térmico ~ cisalhamento vertical do vento real.
E obteve a seguinte equação em coordenadas x, y, p (a dedução pode ser encontrada na bibliografia de referência e vale a pena conferir!):
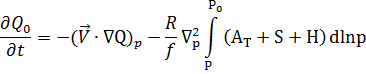 |
Desta maneira, Sutcliffe permitiu associar a taxa de variação de pressão na superfície com grandezas deriváveis das observações de temperatura e vento de radiossondagens. Em outras palavras, a Teoria Quasi-geostrófica permitiu uma simplificação substancial nas equações, relacionando a divergência com a componente vertical da vorticidade absoluta. Como a divergência é uma medida da taxa de adição/remoção de massa de uma coluna atmosférica, é possível obter uma relação entre a variação da pressão de superfície e o campo de vorticidade em diversos níveis verticais. O conceito de desenvolvimento de sistemas está justamente relacionado com esta taxa de variação de pressão na superfície, que quando positiva (negativa) indica formação ou intensificação de um anticiclone (ciclone).
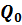 | vorticidade absoluta em 1000 hPa, dada por | 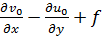 |
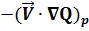 | advecção de vorticidade em 500 hPa (vento e vorticidade deste nível). | |
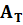 | Advecção de espessura ou de temperatura entre 1000 e 500 hPa, dada por | 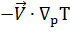 |
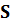 | termo relacionado com o movimento vertical, ou seja, pela estabilidade da coluna de ar, dado por | 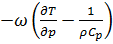 |
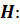 | Taxa de aquecimento médio na camada 1000 - 500 hPa |
É o produto escalar entre os vetores vento e gradiente de vorticidade.
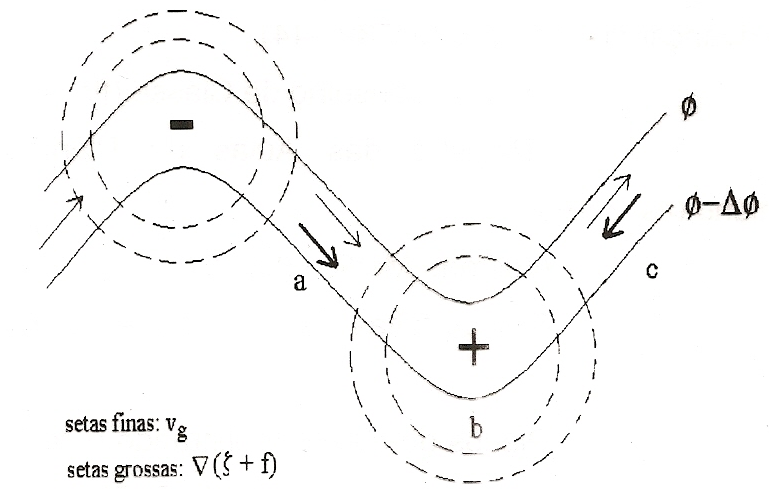 |
| Figura 2 |
Fisicamente, o que acontece a leste do cavado padrão é que está havendo divergência na coluna atmosférica, provocando a diminuição da pressão na superfície. Com isso, ocorrem dois fatos importantes:
É o produto escalar entre os vetores vento e gradiente de temperatura.
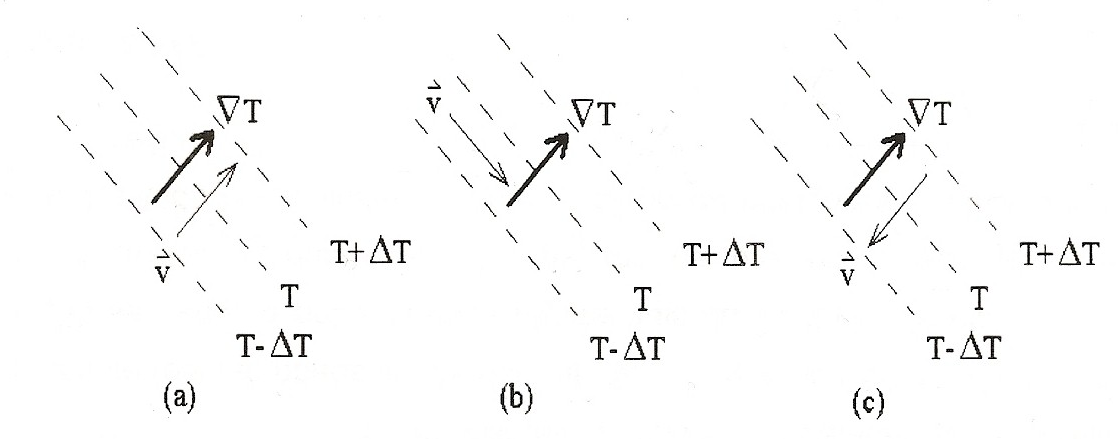 |
| Figura 3 |
É importante observar que o operador laplaciano está aplicado ao termo de advecção de espessura:
A interpretação física deste termo também está ligada à equação hidrostática, pois o ar quente é menos denso do que o ar frio (e portanto vai pesar menos no ponto considerado).
Normalmente se observa um extremo de advecção quente na frente de um ciclone em desenvolvimento e um extremo de advecção fria atrás; como o centro do ciclone deve se movimentar na direção de tendência de pressão mínima, este termo é principalmente importante para o deslocamento do sistema.
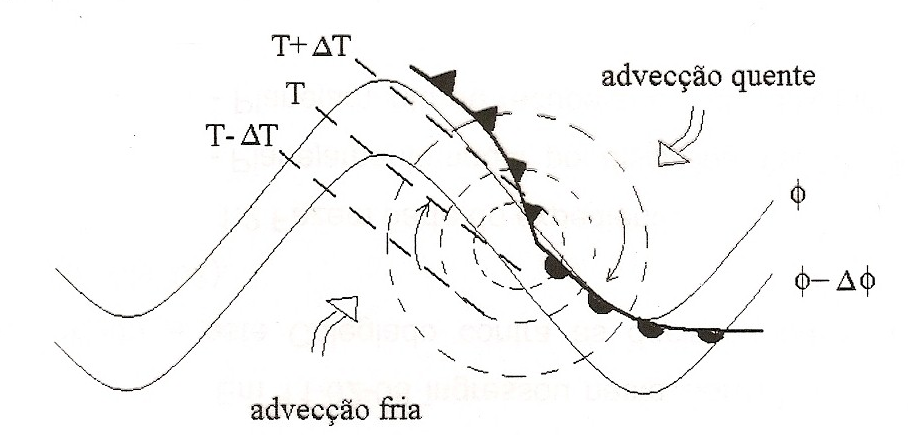 |
| Figura 4 |
Este termo atua de maneira indireta, através da intensificação dos cavados e cristas na média troposfera, realçando assim a advecção de vorticidade.
A avaliação quantitativa deste termo pode ser difícil, tendo em vista que depende de estimativa de divergência. Em geral, o perfil vertical de velocidade vertical apresenta valores extremos na média troposfera e valores bem pequenos próximo à superfície e à tropopausa.
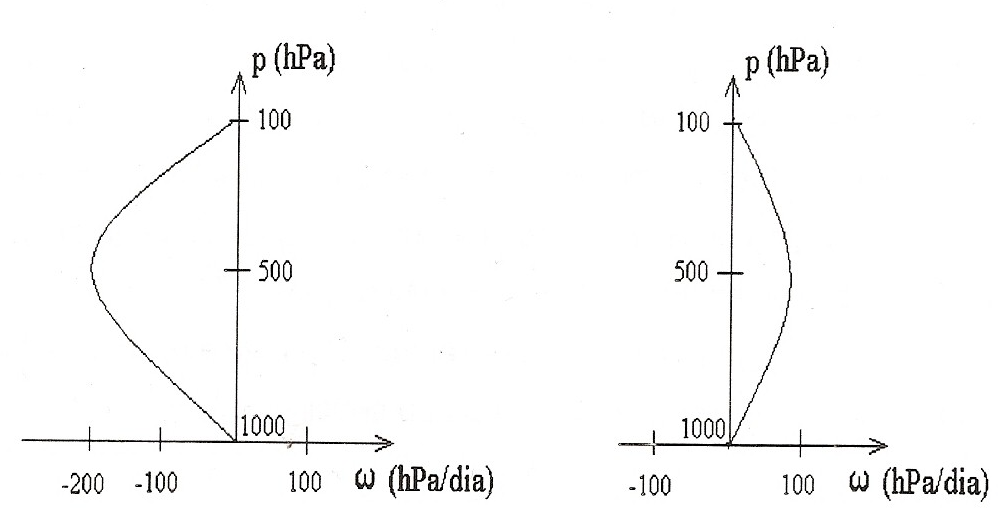 |
| Figura 5 |
Do ponto de vista físico, movimento ascendente (descendente) deve esfriar (esquentar) a parcela por expansão (compressão) adiabática; então, intuitivamente, onde houver subsidência (ascendência) deve haver tendência negativa (positiva) na pressão de superfície.
Para entender a realimentação negativa na intensificação desse sistemas é importante observar que o operador laplaciano também está aplicado ao termo de estabilidade, e como foi visto anteriormente ocorre a inversão do sinal. Como regra prática, para o HS:
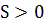 | favorável à ciclogênese |
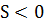 | favorável à anticiclogênese |
Considerando uma atmosfera estável, ou seja,tem-se no HS:
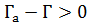 |
Como exemplo prático deste fenômeno, considere a evolução de um anticiclone ao cruzar os Andes:
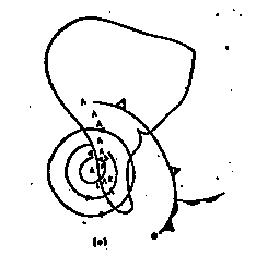 | 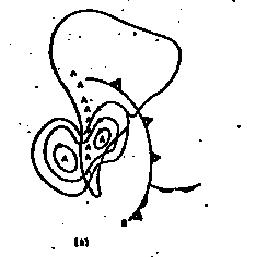 |
| Figura 6 |
É importante avaliar os mecanismos físicos que provocam aquecimento da coluna de ar:
Da teoria quase-geostrófica, após alguma álgebra, é possível obter uma expressão que relacione a tendência do geopotencial com seu respectivo campo tridimensional:
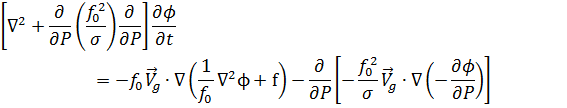 |
| (A) (B) (C) |
Esta equação envolve a distribuição das advecções de espessura (termo C) e de vorticidade (termo B).
O operador laplaciano está aplicado ao termo de tendência do geopotencial implicando numa troca de sinal. Se este termo for maior (menor) que zero implica em tendência do geopotencial menor (maior) que zero.
O termo de advecção de vorticidade absoluta geralmente é a principal forçante na alta troposfera. Este termo não pode por si só promover a intensificação do distúrbio nos níveis onde está ocorrendo, mas atua no sentido de propagar os distúrbios horizontalmente e de espalhá-los na vertical; por isso é conhecido como termo de deslocamento do sistema.
Analisando o sinal a leste do cavado no HS:
OBS1: ondas curtas ou longas em relação ao efeito beta (curtas da ordem de 3.000 km e longas da ordem de 10.000 km).
OBS2: as ondas curtas “carregam” as frentes frias.
É o termo que representa a variação vertical da advecção de espessura (ou advecção diferencial de temperatura) e é mais efetivo na baixa troposfera. Assim como no termo anterior, a resposta da tendência do geopotencial não se limita só ao nível onde está ocorrendo a advecção de temperatura, mas se espalha na vertical.
Para ondas baroclínicas em estágio de desenvolvimento, a advecção de temperatura fria (quente) abaixo do eixo do cavado (crista) em 500 hPa tende a aprofundá-lo (construí-la) pois reduz (aumenta) a espessura da coluna.
Da mesma forma que para a equação da tendência do geopotencial, é possível obter outra expressão que relaciona o movimento vertical com o campo de geopotencial no mesmo instante. A forma mais comum da equação do movimento vertical ou equação Omega é:
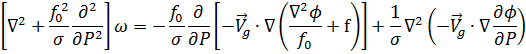 |
| (A) (B) (C) |
Observe que esta equação só envolve derivadas no espaço, sendo portanto uma equação diagnóstica para o movimento vertical a partir do campo de geopotencial. No entanto, como ela envolve derivadas de ordem mais altas do que os demais métodos para estimar movimento vertical, passa a ser de difícil aplicação. A interpretação dos termos será dada a seguir.
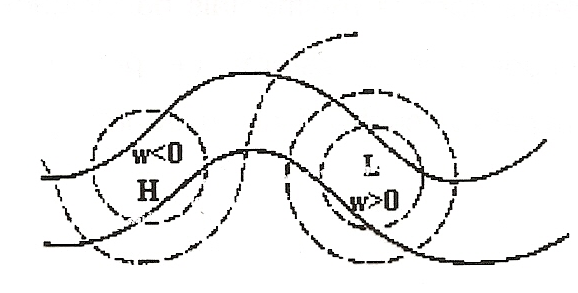 |
| Figura 7 |
Envolve o laplaciano da advecção de espessura, ou então, menos o laplaciano da advecção de temperatura e, portanto:
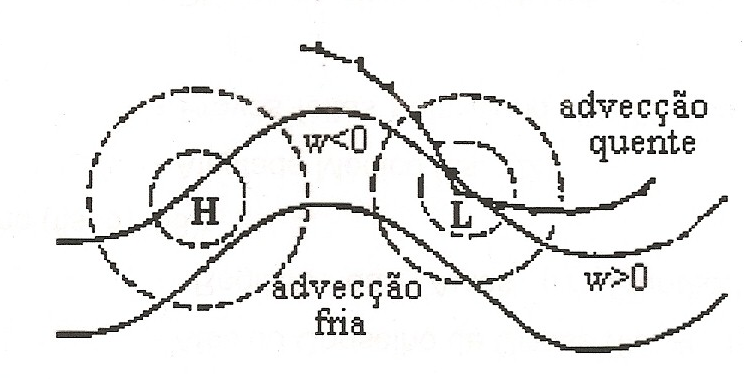 |
| Figura 8 |
Fisicamente, este padrão de movimento vertical é requerido para manter o campo de vorticidade geostrófica nos níveis mais altos, na presença de mudanças na espessura devida a advecção térmica. Por exemplo:
1) Advecção térmica quente aumenta a espessura da camada 500-1000 hPa abaixo da crista em 500 hPa;
2) Intensifica a crista em 500 hPa, o que requer maior vorticidade anticiclônica neste nível para manter o equilíbrio geostrófico;
3) Como na região da crista em 500 hPa não há advecção de vorticidade, é necessário que haja divergência horizontal para compensar a tendência;
4) Por continuidade, deve haver movimento ascendente nos baixos níveis para repor o ar divergente nos níveis superiores.
Apesar dos termos da equação Omega terem um significado conceitual relativamente simples, na prática existe um certo cancelamento entre os termos, e além disso as derivadas de ordem alta envolvidas aumentam muito a imprecisão nas estimativas.
Por isso, existe uma forma alternativa da equação Omega que expressa o movimento vertical em termos da divergência horizontal de um campo vetorial, o qual depende dos gradientes horizontais dos campos de temperatura e vento geostrófico. A equação do vetor Q é:
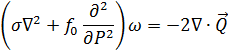 |
Onde:
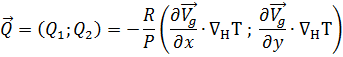 |
o qual pode ser determinado com informações de apenas um nível.
E pelos mesmos argumentos das seções anteriores com respeito ao laplaciano de um campo:
A interpretação física consiste no fato de que é preciso haver movimento ageostrófico e seus respectivos movimentos verticais para manter o balanço do vento térmico no sistema quase geostrófico. Uma expressão bastante usada considerando um caso relativamente simples de isotermas paralelas ao eixo x é:
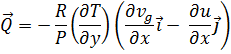 |
Ou:
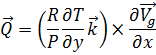 |
Cuja representação esquemática é apresentada a seguir:
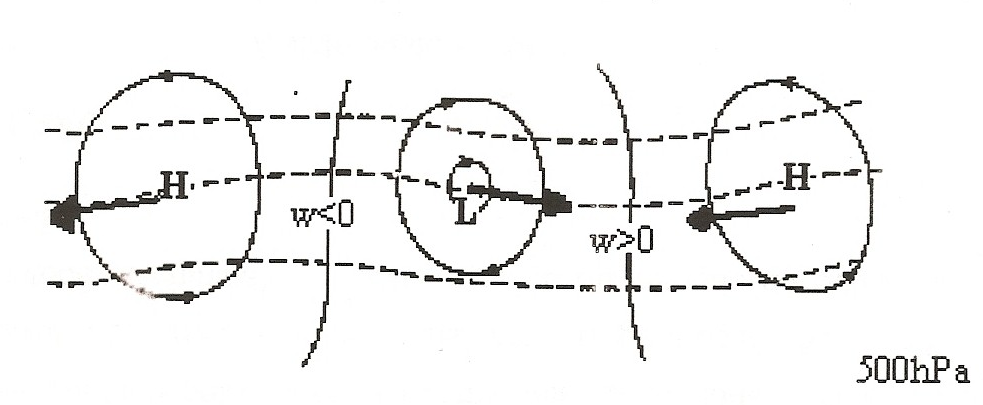 |
| Figura 9 |
Da mesma forma, pode-se avaliar o comportamento do campo vertical considerando a região de entrada de um jato em altitude:
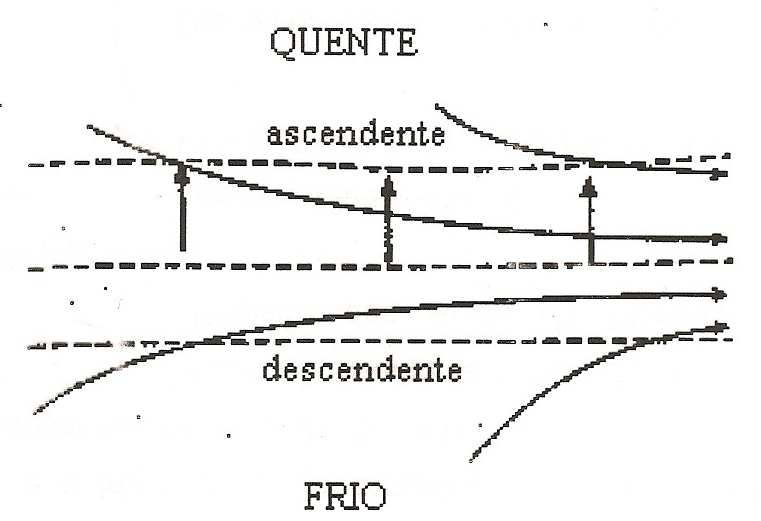 |
| Figura 10 |
1) O que é a Teoria Quase Geostrófica?
2) Quais são as equações do sistema Quase Geostrófico? Por que elas são importantes? Quais são diagnósticas e quais são prognósticas?
3) A Teoria de Sutcliff se baseia em três suposições. Quais são elas? Essa teoria pode ser aplicada em regiões barotrópicas?
4) Analise os termos da equação de Sutcliff:
a) Completando a tabela baixo:
| Favorável a Ciclogênese | Desfavorável a Ciclogênese | ||
|---|---|---|---|
| Tendência da vorticidade absoluta em 1000 hPa | 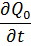 | 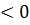 | 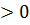 |
| Advecção de vorticidade em 500 hPa | 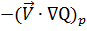 | ||
| Advecção de espessura ou de temperatura entre 1000 e 500 hPa | |||
| Termo de estabilidade | |||
| Taxa de aquecimento médio na camada |
b) O que é nível de não divergência e onde ele situa-se? Qual o cuidado que se deve ter ao analisar a advecção de vorticidade relativa neste nível?
c) Qual o papel do laplaciano para os termos dentro da integral?
d) Por que o termo de advecção de temperatura atua de maneira indireta?
e) Discuta com suas palavras o motivo pelo qual o termo de estabilidade é conhecido como termo de interferência destrutiva da equação.
f) Quais os processos físicos que aquecem a coluna de ar. Por que o calor latente aquece a coluna inteira?
5) Qual o mecanismo de formação de um VCAN de origem subtropical?
6) O que é efeito beta? Por que ele é sempre positivo?
7) Se predominar vorticidade relativa (ondas curtas), para onde se propagam as ondas? E para vorticidade absoluta?
8) Por que nas análises em sala de aula, vemos apenas ondas propagando-se para leste?
9) Qual o sentido físico do termo B na equação da Tendência do Geopotencial? E o termo C?
10) Qual a diferença entre a equação de Tendência do Geopotencial e a Equação Omega?
11) Qual o importância do Vetor Q?
Djuric, Dusan 1994: Weather Analysis - Chapter I, Prentice-Hall Inc.
H.B. Bluestein 1992: Synoptic - Dynamic Meteorology at Midlatitudes, Volume I - Chapter I, Oxford University Press.
Holton, J. R., 1979: An Introduction to Dynamic Meteorology.
Kousky, V.E. & Elias, M.: Meteorologia Sinótica I.
Petersen, 1956: Weather Analysis and Forecasting.
Silva Dias, P.L., 1986: Interpretação da Teoria de Desenvolvimento de Sutcliffe - Curso de Extensão Universitária - Introdução ao uso de modelos diagnósticos para previsão do tempo - DCA/IAG/USP.
Sutcliffe, 1947: QJRMS 73 370-383.